Bife
Active Member
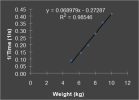
Makes total sense to me - I think its a great benchmark test, very well thought out to be simple and repeatable, yet give good data.If applying enough force (1.2m and 8kg) to test the vcu in its linear zone then it can be quite accurate. One full turn of the vcu is enough to mix the fluid round so its even. If you repeat the test continuouly after this, results will be the same.
I cant do anything about the inevitable variation between different people's tests, but I can make sure its minimised within my tests to make them as repeatable as possible.
Especially as I will mainly use it to see how my VCU degrades (as well as carefully comparing it with other peoples values)
And I like to video tests as its easy with a phone and VLC is simple software
My Freelander specialist mechanic drained and replaced the fluid with his own formulation, so it probably wont behave exactly like everyone else's
And its much hotter here, I use car for short trips infrequently and 95% on the road, although roads are really terrible here (I laugh at your so-called 'potholes'!), my driving style is different, I might be more/or less finicky about the experiment, It might be Friday afternoon, etc etc